Математика

Вміло використовуємо математику при розв’язуванні задач з фізики

При розв’язуванні багатьох задач з фізики з метою швидшого отримання кінцевого результату слід використовувати найпростіші формули наближених розрахунків. Ці формули базуються на наступному твердженні:

для довільних дійсних чисел к та дійсних х, що │х│< 1 справедливою є рівність:  

(1 + x)^к = 1 + k∙x/1 + k(k – 1)∙x²/1·2 + ∙∙∙

У випадку, коли │х│‹ 1, а к є порядку одиниці, то в безмежній сумі можна обмежитись лише двома першими складовими, тобто знехтувати доданками, котрі містять х², х³, …, як безмежно малими величинами.

Тоді

(1 + х)^к ≈ 1 + кх , при х << 1.

Справедливими є наступні формули наближених розрахунків:

(1 + х)² ≈ 1 + 2х

(1 – х)² ≈ 1 – 2х

(1 + х)^-1 ≈ 1 – х

(1 – х)^-1 ≈ 1 + х

(1 + х)^1/2 ≈ 1 + х/2

(1 – х)^1/2 ≈ 1 – х/2

е^+х  ≈ 1 + х

е^-х  ≈ 1 – х

ln(1 + x) ≈ +x

ln(1 – x) ≈ -x

                             sinx ≈ tgx ≈ x,          х < 0,077 рад (4,4º)

cosx ≈ 1 – x²/2

Розрахунок за даними формулами дає наближений результат, відмінний від точного лише на 0,1%.

Приклад:

Обчислити з наближенням, якщо │а│<< А.

(А + а)/(А – а) = (1 + а/А)/(1 – а/А) ≈ 

 ≈ (1 + а/А)(1 + а/А) = (1 + а/А)² ≈ 1 + 2а/А.

Якщо, наприклад, А = 100, а = 1, то (А + а)/(А – а)  ≈ 1,02, а точно (А + а)/(А – а) = 1,020202… 

Доцільно прочитати

• Дивовижні криві.
• Тілесний кут
• Тригонометрія

               Математика для фізиків                  

 

Логармфми 

(основні формули для астрономів)

Розв'язуючи задачі та вправи з фізики та, особливо, з астрономії неможливо обійтись без логарифмів. Основні їх властивості перераховано нижче.

Означення:

Log_aN = x        a^x = N 

Логарифмічні функції (графіки)

Десятковий логарифм:

Log₁₀N = lgN = x        10^x = N 

Натуральний логарифм:

Log_aN = lnN = x        e^x = N 

Основна тотожність логарифмів:

a^log_a^b = b,       b>0

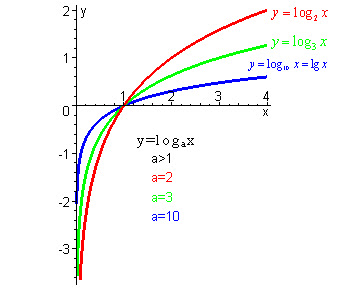Логарифмічні функції (графіки)

Властивості логарифмів:

• log_aa = 1

• log_a1 = 0

• log_a(b · c) = log_ab + log_ac

• log_a(b ⁄ c) = log_ab - log_ac

• log_ax^p = p · log_ax

• log_ax = log_bx ⁄ log_ba  (формула переходу до нової основи)

• log_ab = 1 ⁄ log_ba

• log_ab = log_a^pb^p = p · log_a^pb

• a^log_a^b = b

• log_ca · log_ab = log_cb

• log_a^α b^β = (β⁄α) · log_ab

• a^log_c^b = b^log_c^a

• log_a^α b = log_ab ⁄ log_aa^α = (1 ⁄ α) · log_ab

• log_ca^log_c^b = log_cb^log_c^a

• log_cb · log_ca = log_ca · log_cb

Увага: log(a+b) ≠ log a + log b

Примітка:     e = lim_n→∞(1 + 1/n)ⁿ = e

Варто знати

  

Префікси частинних та кратних одиниць

Приставки ВЕЛИКИХ чисел